The Stokes and Mueller matrices
When the polarization of the incident wave is described by a Stokes vector Si and that of the backscattered wave by a Stokes vector Ss, then the backscattered power from a scatterer is defined by
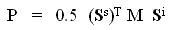 (2-5)
(2-5)
where M is the Stokes matrix, which is a 4x4 array of real numbers  page 291,
page 291,  . In other words, the Stokes matrix is another way of transforming the incident EM wave into the backscattered wave.
. In other words, the Stokes matrix is another way of transforming the incident EM wave into the backscattered wave.
Assuming reciprocity, the Stokes matrix is symmetric, containing 10 different numbers, of which 9 are independent. Each element can be computed from the scattering matrix.
The Mueller matrix is a close relative of the Stokes matrix, except that reciprocity is not assumed and so it contains more independent elements. The Mueller matrix is used in the FSA convention. There is an equivalent form of the power equation (2-5) for the Mueller matrix, and for the covariance and coherency matrices as well.
The Kennaugh matrix K is the version of the Stokes matrix used in the BSA convention. They are related by M = diag[1 1 1 -1] K. The trace of the Kennaugh matrix equals the total power, but the trace of the Mueller matrix does not. The elements of the Kennaugh matrix are defined in  .
.
Remark: Unfortunately, there is inconsistency in the literature about the naming of the matrix M in (2-5). The convention used here comes from page 119 of Raney's chapter in the Manual of Remote Sensing  . The matrix M is called the Stokes scattering operator on page 29 of the Ulaby & Elachi book
. The matrix M is called the Stokes scattering operator on page 29 of the Ulaby & Elachi book  . We assume the conventions used in the Manual of Remote Sensing in this tutorial.
. We assume the conventions used in the Manual of Remote Sensing in this tutorial.
Page details
- Date modified: