The scattering matrix

When a horizontally polarized wave is incident upon a target, the backscattered wave can have contributions in both horizontal and vertical polarizations. The same applies to a vertically polarized incident wave. As the horizontal and vertical components form a complete basis set to describe the electromagnetic wave, the backscattering properties of the target can be completely described by a scattering matrix, S,

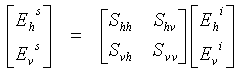    (5)

which describes the transformation of the Electric Field of the incident wave to the Electric Field of the scattered wave (in (1-5), the superscript i refers to the incident wave, and s refers to the scattered wave). Having measured this matrix, the strength and polarization of the scattered wave for an arbitrary polarization of the incident wave can be computed, as any incident wave can be expressed in the [ E_hⁱ , E_vⁱ ] basis set.

The four elements of the scattering matrix are complex, and can be obtained from the magnitudes and phases measured by the four channels of a polarimetric radar. A precise calibration procedure is needed to get the elements, but if the calibration were not necessary, the four scattering matrix elements would be directly measured by the corresponding channels of the radar system. The measured scattering properties of the target apply only at that frequency and radar beam angle used in the mission. However, the scattering properties can vary significantly with radar frequency and beam direction (or rotation of the target), so care should be taken to choose these parameters to be representative of the desired operating scenario.

In monostatic radars, the reciprocity property holds for most targets. This property means that S_hv = S_vh, i.e. the scattering matrix is symmetrical and has only 3 independent elements. Note that as the elements of the scattering matrix are complex, a phase change that may occur during the scattering process can be represented.

Coordinate conventions: The propagation of a plane EM wave is described in a three-dimensional space with the coordinates given by the three axes x, y and z. The z-axis is in the direction of propagation, while the x- and y-axes lie in a plane perpendicular to the direction of propagation, with the (x, y, z) forming a right-hand orthogonal set. In scattering situations, the coordinate space has to be defined for both the incident wave and the scattered wave.

Two conventions have arisen in the literature; the forward scatter alignment (FSA) and the back scatter alignment (BSA. For the FSA, the positive z-axis is in the same direction as the travel of the wave (for both the incident and scattered wave), while in the BSA, the positive z-axis points towards the target for both the incident and scattered wave. Comparing these two cases, the z-axis points in the same direction for the incident wave, but in opposite directions for the scattered wave. For the monostatic radar case, the coordinate systems are the same for the incident and scattered wave in the BSA convention, so the BSA is more commonly used for imaging radars.

Because of the differing convention rules, the scattering matrix takes on a different form in the BSA and FSA conventions. In the BSA convention, the scattering matrix is called the Sinclair matrix, while in the FSA convention, the scattering matrix is called the Jones matrix , page 278.

Whiz quiz

Question: How does the polarization of a scattered EM wave differ between the FSA and BSA conventions? The answer is...

Whiz quiz - answer

Answer: The BSA convention can be viewed as seeing the EM wave from the opposite direction as in the FSA convention. This has the effect of reversing the apparent direction of rotation of the wave and results in a change of sign of the ellipticity of the wave.