Polarimetric data expressed in the power domain
The covariance and coherency matrices
There are many different ways of representing the scattering properties of a target, and they are often expressed in the power domain. Several of the most widely used power representations are introduced in this section.
2.1 The Covariance and Coherency Matrices
The scattering vector or covariance vector kC is a vectorized version of the scattering matrix. Assuming reciprocity, whereby Svh = Shv , this vector is
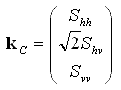 (2-1)
(2-1)
It is convenient to construct a power-domain representation of the scattering properties, which is done by forming the product of this vector with itself. This results in the covariance matrix, which also fully describes the scattering properties of the target target [ ,
,  Section 5-4.10]:
Section 5-4.10]:
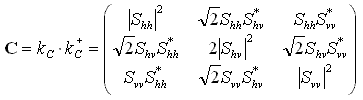 (2-2)
(2-2)
where + denotes conjugate transpose and * the conjugate. The covariance matrix has conjugate symmetry.
The coherency matrix is closely related to the covariance matrix, and is preferred by some analysts  . To obtain the coherency matrix, the scattering matrix is vectorized in a different way using the Pauli spin elements (again assuming reciprocity):
. To obtain the coherency matrix, the scattering matrix is vectorized in a different way using the Pauli spin elements (again assuming reciprocity):
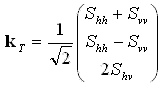 (2-3)
(2-3)
This vector is sometimes preferred because its elements have a physical interpretation (odd-bounce, even-bounce, diffuse, etc.). Note that some authors use (Svv - Shh) for the second element of this vector  , obtaining an equivalent analysis. Again, the information in (2-3) is expressed in the power domain by forming the "product" of this vector with itself, resulting in the coherency matrix:
, obtaining an equivalent analysis. Again, the information in (2-3) is expressed in the power domain by forming the "product" of this vector with itself, resulting in the coherency matrix:
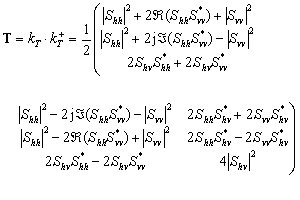 (2-4)
(2-4)
The eigenvalues of the covariance matrix and the coherency matrix are real and are the same. The sum of the diagonal elements (the trace) of both matrices is also the same, and represents the total power of the scattered wave if the incident wave has unit power. Note that most authors use the BSA convention for these definitions.
Page details
- Date modified: