Radar Polarimetry - Polarimetric Parameters
When polarimetric radar data is analyzed, there are a number of parameters that can be computed that have a useful physical interpretation ![]() . They can be computed for every sample in a polarimetric radar image, but are often averaged over groups of samples to reduce the effect of noise.
. They can be computed for every sample in a polarimetric radar image, but are often averaged over groups of samples to reduce the effect of noise.
When polarimetric radar data is analyzed, there are a number of parameters that can be computed that have a useful physical interpretation ![]() . They can be computed for every sample in a polarimetric radar image, but are often averaged over groups of samples to reduce the effect of noise.
. They can be computed for every sample in a polarimetric radar image, but are often averaged over groups of samples to reduce the effect of noise.
Total Power
A quantity giving the total power received by the four channels of a polarimetric radar system. In terms of the Sinclair (scattering) matrix, the total power equals |Shh|2 + |Shv|2 + |Svh|2 + |Svv|2
The power received by a polarimetric radar can be expressed by the covariance, coherence or Kennaugh matrices. The total power in the four channels is proportional to the sum of the diagonal elements or trace of these matrices.
Co-pol Correlation Coefficient
The correlation between the two co-polarized channels in a multi-polarized or polarimetric radar.
The co-pol channels are often HH and VV. The correlation coefficient is complex and is computed as the average of the product between the complex amplitude of the HH channel and the conjugate of the complex amplitude of the VV channel. It is normalized by the square root of the product of the powers in the HH and VV channels ![]()
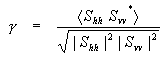 (equation 4-1)
(equation 4-1)
If the magnitude of the correlation coefficient is unity, the received signals from the two channels are linearly related (i.e. one can be computed from the other). An example is the backscatter received from an ideal trihedral corner reflector. If the magnitude of the correlation coefficient is less than one, it means that the backscattering at HH and VV are not directly related. It also may mean that noise is present on one or both of the channels or the received EM waves are partially polarized. It is possible to compensate the coefficient for the receiver noise in the radar system ![]() , page 294.
, page 294.
Co-pol Phase Difference
The phase difference between the two co-polarized channels in a multi-polarized or polarimetric radar. It is the phase angle of the co-pol correlation coefficient. Note that when averaging is performed, the coherent scattering matrix elements are averaged, and then the co-pol phase difference is calculated from the average.
Often the co-pol channels are HH and VV, and the co-pol phase difference is the average difference between the phase angles of the corresponding pixels (or group of pixels) in the HH and the VV channels. The co-pol phase difference is often helpful in classifying a pixel, as it is characteristic of the number of bounces that the EM wave experiences during reflection. An ideal single-bounce (or odd-bounce) scatterer will have a co-pol phase difference of 180° in the BSA convention, while an ideal double-bounce (or even-bounce) scatterer will have a co-pol phase difference of 0°.
In practical situations, there will be a fair amount of variation in the co-pol phase difference measurements. A surface with a small amount of roughness (i.e. not too rough such that multi-bounce scattering would occur) will backscatter with a co-pol phase difference near 180°, and an open upright structure like a telephone pole will have a co-pol phase difference near zero. However, backscatter from an agricultural field could have a variety of co-pol phase difference values between -180° and 180°, depending upon the size, spacing and type of vegetation. For example, backscatter from a cornfield with well-defined vertical stalks is expected to have a significantly lower co-pol phase difference than a field of peas (depending upon the radar frequency).
There is also a "cross-pol phase difference", with the analogous definition. However, the cross-pol phase difference is usually very random, as there is generally little correlation between the scattering phase centres of the HH and HV channels (for example). If a scene-dependent pattern is observed in the cross-pol phase difference, it is likely due to channel cross-talk that has not been corrected in the processing.
Degree of Polarization
The degree of polarization is given by the ratio of the power in the polarized part of an electromagnetic wave to the total power in the electromagnetic wave.
An electromagnetic wave can have a polarized and a non-polarized component, and the Stokes parameters are a convenient way of expressing the powers in each of the two parts. The total power in the wave is given by the Stokes parameter S0, while ![]() gives the total power in the polarized part. Accordingly, the degree of polarization can be expressed in terms of the Stokes parameters:
gives the total power in the polarized part. Accordingly, the degree of polarization can be expressed in terms of the Stokes parameters:
![]() ( equation 4-2)
( equation 4-2)
Coefficient of Variation
The normalized ratio between the maximum and minimum power in a polarization signature (Pmax - Pmin) / Pmax.
When the coefficient of variation equals one, the signature has a null at some polarization, and the received signal is fully polarized. When the coefficient equals zero, the polarization signature is flat and the received signal is unpolarized (e.g. all noise). The coefficient of variation is also called the fractional polarization ![]() .
.
Page details
- Date modified: