The polarization state

The polarization state of a plane wave can be described by orientation and ellipticity, plus a parameter S₀ that is proportional to the total intensity of the wave. Writing the horizontal and vertical components of the Electric Field vector as E_h and E_v, the British physicist, Gabriel Stokes, described the polarization state of the EM wave by a 4-element vector, [ S₀, Q, U V ] ^T, now known as the Stokes vector:

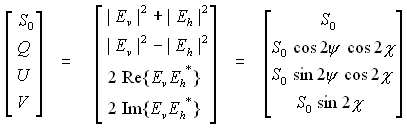    (1)

where | . | is the absolute value and * is the complex conjugate. An electromagnetic plane wave can be completely polarized, partially polarized or completely unpolarized. In the completely polarized case, only 3 of the Stokes parameters are independent, because of the total power relation:

    (2)

For a completely polarized wave, the polarization state can be described by a point on the Poincaré sphere, as shown in Figure 1-8. The radius of the sphere is S₀, the intensity of the wave. The latitude of a point on the sphere corresponds to 2, i.e. two times the ellipticity of the wave.

Did you Know?

The British physicist, George Gabriel Stokes, was born on August 13, 1819 in Skreen, County Sligo, Ireland, and became a professor at Cambridge in 1849, a position he held until his death on February 1, 1903 (the centennial is soon). In addition to his work with polarimetry and the theory of light, he is also known for his research in fluid mechanics, spectrum analysis, geodesy, and the theory of sound and vector calculus. He was elected as a member of the Royal Society in 1851, and was its president from 1885 to 1890. He was also a member of the British Parliament from 1887 to 1892, noted for supporting educational issues.

The longitude of a point on the sphere corresponds to 2, i.e. two times the orientation of the wave.

We can see from this notation that linear polarizations lie on the equator, with horizontal and vertical polarizations opposite each other. Left-hand circular and right-hand circular polarizations lie on the north and south poles respectively. All other points on the sphere represent elliptical polarizations of various ellipticities () and orientations (). Points on the sphere that are directly opposite one another represent polarizations that are orthogonal to one another, and are referred to as cross polarizations.

If the electromagnetic wave is partially polarized, it can be expressed as the sum of a completely polarized wave and a completely unpolarized or noise-like wave. The degree of polarization is the ratio of the polarized power to the total power, and in terms of the Stokes parameters, the degree of polarization is given by

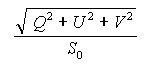    (3)

so that for partially polarized waves, the total power is greater than the polarized power:

    (4)

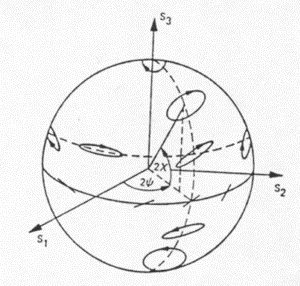
Figure 1-8: Orientation and ellipticity of a fully polarized wave represented on the Poincaré sphere.

Whiz quiz

Question: If an EM wave is horizontally polarized, what is the corresponding orthogonal polarization? The answer is...

Whiz quiz - answer

Answer: The orthogonal or cross polarization to linear horizontal is linear vertical polarization. Two orthogonal polarizations can form a basis set, used to describe the polarization of an EM wave. Linear horizontal and linear vertical are two orthogonal polarizations that are commonly used as the basis set, but left-hand circular and right-hand circular are sometimes chosen as basis set.