The polarization ellipse
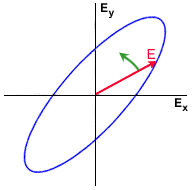
The Electric Field of a plane wave can be described as the vector sum of two orthogonal components, typically horizontal and vertical components. The two components are characterized by their amplitudes and the relative phase between them. When viewed along its direction of propagation, the tip of the Electric Field vector of a fully polarized wave traces out a regular pattern. In its most general form, the pattern is an ellipse, as shown in Figure 1-2.
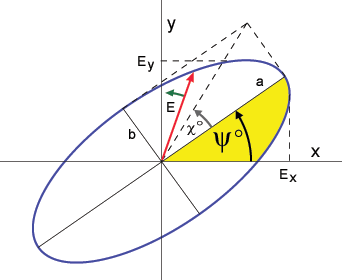
Figure 1-2: Polarization ellipse showing the orientation angle 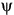 and ellipticity
and ellipticity 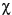 , which are a function of the semi-major and semi-minor axes, a and b
, which are a function of the semi-major and semi-minor axes, a and b
The ellipse has a semi-major axis of length a, and a semi-minor axis of length b. The angle of the semi-major axis, measured counter-clockwise from the positive horizontal axis, is the "orientation", 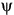 , of the EM wave, and can take on values between 0° and 180°. The degree to which the ellipse is oval is described by a shape parameter called eccentricity or ellipticity, defined as
, of the EM wave, and can take on values between 0° and 180°. The degree to which the ellipse is oval is described by a shape parameter called eccentricity or ellipticity, defined as 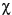 = arctan(b/a), which can take values between -45° and +45°.
= arctan(b/a), which can take values between -45° and +45°.
The shape of the ellipse is governed by the magnitudes and relative phase between the horizontal and vertical components of the Electric Field vector. Figure 1-3 illustrates the effect of relative phase between the components, when the magnitudes of the components are equal. When the components are in phase, the polarization is linear (ellipticity 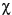 = 0), with an orientation of 45°. As the relative phase angle increases to
= 0), with an orientation of 45°. As the relative phase angle increases to 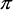 /2 radians, the orientation remains at 45°, but the ellipticity increases to 45°, representing circular polarization. This sequence is shown in the top row of Figure 1-3 (plus the first entry in the second row), where the phase in increased in steps of
/2 radians, the orientation remains at 45°, but the ellipticity increases to 45°, representing circular polarization. This sequence is shown in the top row of Figure 1-3 (plus the first entry in the second row), where the phase in increased in steps of 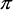 /8.
/8.
Then as the relative phase increases from 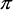 /2 to 3
/2 to 3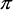 /2 radians, the orientation flips to 135°, and the ellipticity goes from 45° to zero then to -45°. This sequence is shown in rows 2 and 3 of the figure (plus the first entry in the fourth row). Finally in row 4, the relative phase goes from 3
/2 radians, the orientation flips to 135°, and the ellipticity goes from 45° to zero then to -45°. This sequence is shown in rows 2 and 3 of the figure (plus the first entry in the fourth row). Finally in row 4, the relative phase goes from 3
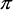 /2 to 15
/2 to 15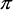 /8, the orientation flips to +45°, and the ellipticity tends to zero again.
/8, the orientation flips to +45°, and the ellipticity tends to zero again.

Figure 1-3: The shape of the polarization ellipse as the relative phase between the horizontal and vertical components of the Electric Field vector is varied from 0 to 15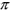 /8 radians in steps of
/8 radians in steps of 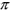 /8
/8
Larger Image
Figure 1-3 illustrates how a circle and a straight line are limiting cases of the ellipse. If the phase angle between the horizontal and vertical components is zero or 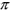 radians, the ellipse becomes a straight line. In this case, the ellipticity is zero and the polarization is referred to as "linear".
radians, the ellipse becomes a straight line. In this case, the ellipticity is zero and the polarization is referred to as "linear".
 Did you Know?
Did you Know?
Did you know that a fully polarized wave could be made up of sine waves of many frequencies? However, in SAR system analysis, we usually assume a single frequency or "monochromatic sine wave". This is a valid assumption, as SAR systems usually have a very narrow bandwidth (compared to the carrier frequency) so that the transmitted wave can be approximated by a sine wave.
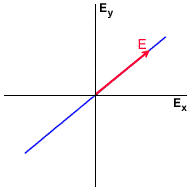
Figure 1-3 assumes that the magnitudes of the horizontal and vertical components are equal, but if they are not equal, the orientation can take on any value between 0 and 180°. If the ellipticity is zero and the orientation is 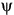 = 0 (180° is equivalent), the polarization is horizontal linear (the vertical component is zero), and if
= 0 (180° is equivalent), the polarization is horizontal linear (the vertical component is zero), and if 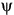 = 90°, the polarization is vertical linear (the horizontal component is zero). These are the two linear polarizations in common use.
= 90°, the polarization is vertical linear (the horizontal component is zero). These are the two linear polarizations in common use.
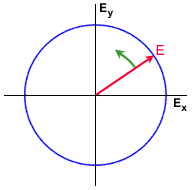
If the phase angle between the horizontal and vertical components is 90°, and the horizontal and vertical components are equal, the ellipse becomes a circle. In this case, the ellipticity has a magnitude of 45°, and the orientation is not defined. An ellipticity of 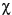 = +45° corresponds to a left circular polarization and
= +45° corresponds to a left circular polarization and 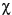 = -45° corresponds to a right circular polarization. If the wave is observed along the direction of propagation, the polarization is left-handed if the rotation of the Electric Field vector is counter-clockwise.
= -45° corresponds to a right circular polarization. If the wave is observed along the direction of propagation, the polarization is left-handed if the rotation of the Electric Field vector is counter-clockwise.
Examples of linear, elliptical and circular polarizations are shown in the figures, where the rotation of the Electric Field vector is also shown.
Whiz quiz

Question: Why are the horizontal and vertical components sufficient to describe the polarization of an EM wave? The answer is...
Whiz quiz - answer

Answer: The polarization of a plane EM wave is described by the locus of its Electric Field vector in a plane perpendicular to the direction of propagation. Two orthogonal components are required to describe the location of the vector in the plane, and horizontal and vertical components, Ex and Ey (or Eh and Ev) are the most convenient ones to use.
Page details
- Date modified: