Supervised Bayes Maximum Likelihood Classification

An alternative to the model-based approach is to define classes from the statistics of the image itself. The classes are defined by an operator, who chooses representative areas of the scene to define the mean values of parameters for each recognizable class (hence it is a "supervised" method). A probabilistic approach is useful when there is a fair amount of randomness under which the data are generated. Knowledge of the data statistics (i.e. the theoretical statistical distribution) allows the use of the Bayes maximum likelihood classification approach that is optimal in the sense that, on average, its use yields the lowest probability of misclassification .

After the class statistics are defined, the image samples are classified according to their distance to the class means. Each sample is assigned to the class to which it has the minimum distance. The distance itself is scaled according to the Bayes maximum likelihood rule.

Bayes classification for polarimetric SAR data was first presented in 1988 . The authors showed that the use of the full polarimetric data set gives optimum classification results. The algorithm was only developed for single-look polarimetric data, though. For most applications in radar remote sensing, multi-looking is applied to the data to reduce the effects of speckle noise. The number of looks is an important parameter for the development of a probabilistic model.

The full polarimetric information content is available in the scattering matrix S, the covariance matrix C, as well as the coherency matrix T. It has been shown that T and C are both distributed according to the complex Wishart distribution . The probability density function (pdf) of the averaged samples of T for a given number of looks, n, is

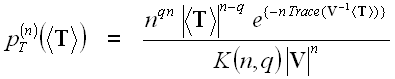(7.1)

where:

• <T> is the sample average of the coherency matrix over n looks,
• q represents the dimensionality of the data (3 for reciprocal case, else 4),
• Trace is the sum of the elements along the diagonal of a matrix,
• V is the expected value of the averaged coherency matrix, E{<T>}, and
• K(n,q) is a normalization factor.

To set up the classifier statistics, the mean value of the coherency matrix for each class V_m must be computed

(7.2)

where _m is the set of pixels belonging to class m in the training set.

According to Bayes maximum likelihood classification a distance measure, d, can be derived :

(7.3)

where the last term takes the a priori probabilities P(_m) into account. Increasing the number of looks, n, decreases the contribution of the a priori probability. Also, if no information on the class probabilities is available for a given scene, the a priori probability can be assumed to be equal for all classes. An appropriate distance measure can then be written as :

(7.4)

which leads to a look-independent minimum distance classifier:

(7.5)

Applying this rule, a sample in the image is assigned to a certain class if the distance between the parameter values at this sample and the class mean is minimum. The look-independence of this scheme allows its application to multi-looked as well as speckle-filtered data . This classification scheme can also be generalized for multi-frequency fully polarimetric data provided that the frequencies are sufficiently separated to ensure statistical independence between frequency bands .

The classification depends on a training set and must therefore be applied under supervision. It is not based on the physics of the scattering mechanisms, which might well be considered a disadvantage of the scheme. However, it does utilize the full polarimetric information and allows a look-independent image classification.

Note that the covariance matrix can also be used for this type of Bayes classification. The coherency matrix was chosen for the simple reason of compliance with the H / A / -classifier described in the previous section.