Polarization Signatures
Because the incident wave can take on so many polarizations, and the scattering matrix consists of 4 complex numbers, it is helpful to have a graphical method of visualizing the response of a target as a function of the incident and backscattered polarizations. One such visualization is provided by the polarization signature of the target  .
.
The scattering power can be determined as a function of the four wave polarization variables, the incident 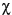 and
and 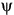 and backscattered
and backscattered 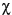 and
and 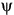 angles, but these constitute too many independent variables to observe conveniently. To simplify the visualization, the backscattered polarizations are restricted to be either the same polarization or the orthogonal polarization as the incident wave. This choice of polarization combinations leads to the calculation of the co-polarized and cross-polarized responses for each incident polarization, which are portrayed in two surface plots called the co-pol and cross-pol signatures. These two signatures do not represent every possible transmit-receive polarization combination, but do form a useful visualization of the target's backscattering properties
angles, but these constitute too many independent variables to observe conveniently. To simplify the visualization, the backscattered polarizations are restricted to be either the same polarization or the orthogonal polarization as the incident wave. This choice of polarization combinations leads to the calculation of the co-polarized and cross-polarized responses for each incident polarization, which are portrayed in two surface plots called the co-pol and cross-pol signatures. These two signatures do not represent every possible transmit-receive polarization combination, but do form a useful visualization of the target's backscattering properties  ,
,  . The BSA convention is usually used for the signatures.
. The BSA convention is usually used for the signatures.
An incident electromagnetic wave can be selected to have an Electric Field vector with an ellipticity 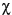 between -45° and +45°, and an orientation
between -45° and +45°, and an orientation 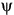 between 0° and 180°. These variables are mapped along the x- and y-axes of a 3-D plot portraying the polarization signature. For each of these possible incident polarizations, the strength of the backscatter can be computed for the polarization that is the same as the incident polarization (giving the co-pol signature plot) and for the polarization that is orthogonal to the incident polarization (giving the cross-pol signature plot). For an incident wave of unit amplitude, the power of the co-polarized (or cross-polarized) component of the scattered wave is presented as the z value on the plots. Often the plots are normalized to have a peak value of one.
between 0° and 180°. These variables are mapped along the x- and y-axes of a 3-D plot portraying the polarization signature. For each of these possible incident polarizations, the strength of the backscatter can be computed for the polarization that is the same as the incident polarization (giving the co-pol signature plot) and for the polarization that is orthogonal to the incident polarization (giving the cross-pol signature plot). For an incident wave of unit amplitude, the power of the co-polarized (or cross-polarized) component of the scattered wave is presented as the z value on the plots. Often the plots are normalized to have a peak value of one.
The polarization plots have peaks at polarizations that give rise to maximum received power, and valleys where the received power is smallest, in agreement with the concept of Huynen's polarization fork in the Poincaré sphere. Polarization signatures and the Poincaré sphere can be conveniently drawn on polarimetric analysis workstations. One example is the PWS software for PCs.
Figure 5-1 shows the polarization signatures of the simplest class of targets - a large conducting sphere, a flat plate or a trihedral corner reflector. The wave is backscattered with the same polarization, except for a change of sign of the ellipticity (or in the case of linear polarization, a change of the phase angle between Eh and Ev of 180°). The sign changes once for every reflection - the sphere represents a single reflection, and the trihedral gives three reflections, so each behaves as an "odd-bounce" reflector.
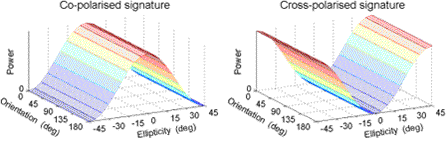
Figure 5-1: Polarization signatures of a large conducting sphere or trihedral corner reflector
For more complicated targets, the polarization signature takes on different characteristic shapes. Interesting signatures are obtained from a dihedral corner reflector and from Bragg scattering off the sea surface. In the case of the dihedral reflector, when its corner (the intersection of its sides) is aligned horizontally, parallel to the horizontal axis of the EM wave, the co-pol response is a maximum for linear or elliptical horizontal, linear or elliptical vertical and circular polarizations (Figure 5-2). Because the two reflecting surfaces of the dihedral sides negate the sign of the ellipticity a second time, this results in a typical "double-bounce" or "even-bounce" signature.
However, if the reflector is rotated by 45° around the radar line of sight, the linear horizontal co-pol response is zero and the linear horizontal cross-pol response is a maximum. This property means that the dihedral can be used as a simple way of creating a cross-pol response in an HH radar system.
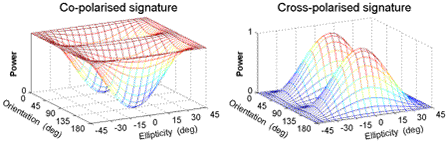
Figure 5-2: Polarization signatures of a dihedral or double-bounce reflector
In the case of Bragg scattering, the response has a ridged shape similar to the single-bounce sphere, except that the backscatter of the vertical polarization is higher than that of the horizontal polarization (see Figure 5-3). The co-pol response has a peak at orientation angle 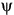 = 90° and at ellipticity angle
= 90° and at ellipticity angle 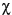 = 0°.
= 0°.
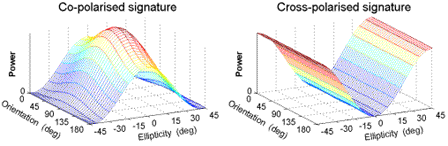
Figure 5-3: Polarimetric signatures of Bragg scattering from the sea surface (Syy = 1.2*Sxx)
The pedestal height is a useful parameter that can be obtained from polarization signatures. The pedestal height is the minimum value of intensity found on the signature, when the maximum response is normalized to unity. The height of the pedestal is an indicator of the presence of an unpolarized scattering component in the received signal, and thus is related to the degree of polarization of a scattered wave. If a single target is scattering and the backscattered wave is fully polarized, or if the signature is calculated from a single unaveraged measurement, the pedestal height is zero. But if the signature is calculated from an average of several samples, and there are multiple, dissimilar scatterers present or there is noise in the received signal, the pedestal height will be non-zero. Thus the pedestal height is also a measure of the number of different types of scattering mechanism found in the averaged samples.
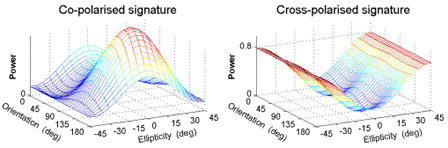
Figure 5-4: Polarization signature of a target having a pedestal height of about 0.2
Whiz quiz

Question 1: Why does the polarization signature of a simple reflector such as a sphere have a ridge-like appearance? The answer is...
Question 2: The polarization signature can have a "pedestal". What does this mean? The answer is...
Question 3: What is the main use of polarization signatures? The answer is...
Whiz quiz - answer

Answer 1: You might expect the co-polarized response to be unity for all incident polarizations, and the cross-polarized response to be zero, but the change of sign of the ellipticity causes the signatures to have the "ridge" and "valley" shapes shown. The co-pol response is unity and the cross-pol response is zero for all linear polarizations (where the change of sign has no effect). But for circular polarizations such as RR, the co-pol response is zero and the cross-pol response of the target is unity. This "change of sign" property is a function of the coordinate frame convention used, and applies to the BSA convention .
Answer 2: A polarization signature computed from a single observation (i.e. a single sample of a polarimetric radar system) represents a fully polarized wave, even though multiple scattering types and noise are present in the measurement. This is because a single observation does not have enough degrees of freedom to represent more than a single pure scattering mechanism. As the scattered wave is assumed to be fully polarized, the signature will be zero for at least one combination of transmit and receive polarization.
However, when the Stokes matrices of adjacent pixels are averaged, the net response will contain components from more than one type of scatterer and noise as well, assuming that the individual Stokes matrices are not identical  . In this case, the minimum of the polarization signature will not be zero, but a certain positive value. This gives the polarization signature the appearance of "sitting on a pedestal". The height of the pedestal depends upon how different the various scattering mechanisms are present in the averaged pixels, or how much noise is present in the observations.
. In this case, the minimum of the polarization signature will not be zero, but a certain positive value. This gives the polarization signature the appearance of "sitting on a pedestal". The height of the pedestal depends upon how different the various scattering mechanisms are present in the averaged pixels, or how much noise is present in the observations.
Answer 3: Polarization signatures are one way of visualizing the backscatter behaviour of a target. The polarization signature of a pixel in an image can be related to the signatures of known elemental targets, making it possible to infer the type of scattering that is taking place.
When pixels in an image are averaged, the net response will contain components from more than one type of scatterer and noise as well. When analyzed in the power domain, these scattering components are additive. If we are lucky, we can relate the composite signature to known elemental signatures, and deduce the types of terrain in the image  .
.
Page details
- Date modified: