Unsupervised Classification Based on H/A/α Parameters
In any classifier, the choice of parameters is important, and in the case of polarimetric radar data, content-independent scattering models can be used to get parameters that provide reasonable class separation. A current example is the H / A / 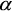 set of parameters derived from an eigenvalue decomposition of the coherency matrix. The H / A /
set of parameters derived from an eigenvalue decomposition of the coherency matrix. The H / A / 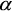 algorithm was developed by Cloude and Pottier, who showed that terrain classes sometimes produced distinct clustering in the H /
algorithm was developed by Cloude and Pottier, who showed that terrain classes sometimes produced distinct clustering in the H / 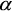 plane
plane  .
.
The H / 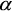 plane is drawn in Figure 7-1. The observable alpha values for a given entropy are bounded between curves I and II (i.e. the shaded areas are not valid). This because the averaging of the different scattering mechanisms (i.e. averaging of the different eigenvectors) restricts the range of the possible a values as the entropy increases. As H and
plane is drawn in Figure 7-1. The observable alpha values for a given entropy are bounded between curves I and II (i.e. the shaded areas are not valid). This because the averaging of the different scattering mechanisms (i.e. averaging of the different eigenvectors) restricts the range of the possible a values as the entropy increases. As H and  are both invariant to the type of polarization basis used, the H /
are both invariant to the type of polarization basis used, the H /  plane provides a useful representation of the information in the coherency matrix
plane provides a useful representation of the information in the coherency matrix  .
.
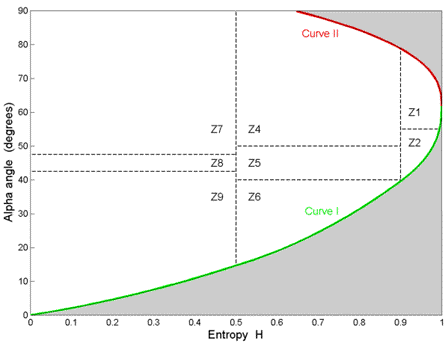
Figure 7-1: The H / 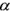 plane showing the model-based classes and their partitioning. A description of the classes (Z1 - Z9) is given in the text.
plane showing the model-based classes and their partitioning. A description of the classes (Z1 - Z9) is given in the text.
The bounds shown in Figure 7-1 (Curve I and Curve II) show that when the entropy is high, the ability to classify different scattering mechanisms is very limited. An initial partition into nine classes (eight usable) has been suggested by Cloude and Pottier  , and is shown in Figure 7-1. Classes are chosen based on general properties of the scattering mechanism and do not depend up on a particular data set. This allows an unsupervised classification based on physical properties of the signal. The class interpretations suggested by Cloude and Pottier are as follows (see
, and is shown in Figure 7-1. Classes are chosen based on general properties of the scattering mechanism and do not depend up on a particular data set. This allows an unsupervised classification based on physical properties of the signal. The class interpretations suggested by Cloude and Pottier are as follows (see  for more details):
for more details):
- Class Z1: Double bounce scattering in a high entropy environment
- Class Z2: Multiple scattering in a high entropy environment (e.g. forest canopy)
- Class Z3: Surface scattering in a high entropy environment (not a feasible region in H /
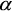 space)
space) - Class Z4: Medium entropy multiple scattering
- Class Z5: Medium entropy vegetation (dipole) scattering
- Class Z6: Medium entropy surface scattering
- Class Z7: Low entropy multiple scattering (double or even bounce scattering)
- Class Z8: Low entropy dipole scattering (strongly correlated mechanisms with a large imbalance in amplitude between HH and VV)
- Class Z9: Low entropy surface scattering (e.g. Bragg scatter and rough surfaces)
It is important to note, however, that the boundaries are somewhat arbitrary and do depend upon the radar calibration, the measurement noise floor and the variance of the parameter estimates. Nevertheless, this classification method is linked to physical scattering properties, making it independent of training data sets. The number of classes needed as well as the usability of the method depends upon the application. Additional interpretation of the classes is given in  , where a small change in the class boundaries is proposed.
, where a small change in the class boundaries is proposed.
The third variable of polarimetric anisotropy has been used to distinguish different types of surface scattering. The H / A-plane representation for surface scattering is given in Figure 7-2, where the shaded region is not feasible. The line delineating the feasible region can be calculated using a diagonal coherency matrix with small minor eigenvalues 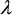 2 and
2 and 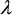 3, with
3, with 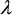 3 varying from 0 to
3 varying from 0 to 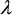 2.
2.
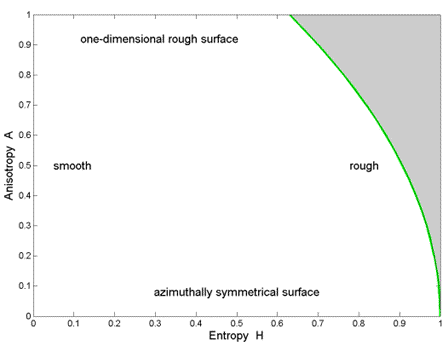
Figure 7-2 Types of surface scattering in the Entropy/Anisotropy plane.
Introduction of the anisotropy to the feature set represents a third parameter that can be used in the classification. One approach is to simply divide the space into two H / 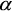 planes using the green plane shown in the 3-D space of Figure 7-3, one side for A
planes using the green plane shown in the 3-D space of Figure 7-3, one side for A 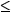 0.5 the other side for A > 0.5. This introduces 16 classes if the H /
0.5 the other side for A > 0.5. This introduces 16 classes if the H / 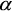 planes are divided according to Figure 7-1. Note that the upper limit of H is restricted when A > 0, as shown in Figure 7-2.
planes are divided according to Figure 7-1. Note that the upper limit of H is restricted when A > 0, as shown in Figure 7-2.
The H / A / 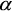 -classification space, given in Figure 7-3, now provides additional ability to distinguish between different scattering mechanisms. For example, high entropy and low anisotropy (
-classification space, given in Figure 7-3, now provides additional ability to distinguish between different scattering mechanisms. For example, high entropy and low anisotropy (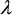 2
2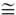
 3) correspond to random scattering whereas high entropy and high anisotropy (
3) correspond to random scattering whereas high entropy and high anisotropy ( 2 >>
2 >>  3) indicate the existence of two scattering mechanisms with equal probability.
3) indicate the existence of two scattering mechanisms with equal probability.
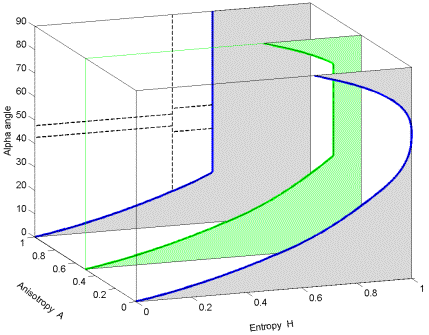
Figure 7-3: Illustration of how an A = 0.5 plane (green) creates 16 classes from the original 8 H / 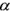 classes shown in Figure 7-1. This gives 16 regions in the Entropy / Anisotropy /
classes shown in Figure 7-1. This gives 16 regions in the Entropy / Anisotropy / 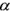 space for use in an unsupervised classifier.
space for use in an unsupervised classifier.
The three parameters H, A and 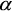 are based on eigenvectors and eigenvalues of a local estimate for the 3x3 Hermitian coherency matrix ("Hermitian" means a square matrix that has conjugate symmetry - it has real eigenvalues). The basis invariance of the target decomposition makes these three parameters roll invariant, i.e. the parameters are independent of rotation of the target about the radar line of sight. It also means that the parameters can be computed independent of the polarization basis.
are based on eigenvectors and eigenvalues of a local estimate for the 3x3 Hermitian coherency matrix ("Hermitian" means a square matrix that has conjugate symmetry - it has real eigenvalues). The basis invariance of the target decomposition makes these three parameters roll invariant, i.e. the parameters are independent of rotation of the target about the radar line of sight. It also means that the parameters can be computed independent of the polarization basis.
Estimation of the three parameters H, A and 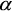 allows a classification of the scene according to the type of scattering process within the sample (H, A) and the corresponding physical scattering mechanism (
allows a classification of the scene according to the type of scattering process within the sample (H, A) and the corresponding physical scattering mechanism (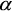 ). The data need to be averaged in order to allow an estimation of H, A and
). The data need to be averaged in order to allow an estimation of H, A and 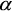 (without averaging, the coherency matrix has rank 1), which has the benefit of reducing speckle noise
(without averaging, the coherency matrix has rank 1), which has the benefit of reducing speckle noise  .
.
An example of the clustering of pixels from a sea ice SIR-C scene is shown in Figure 7-4a  . The H/A plane shows evidence of clustering into two and possibly three classes. Figure 7-4b shows the distribution of H/
. The H/A plane shows evidence of clustering into two and possibly three classes. Figure 7-4b shows the distribution of H/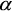 values for a white spruce field; the target shows a dominant dipole scattering (
values for a white spruce field; the target shows a dominant dipole scattering (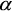 about 45°), with a high value of entropy H of about 0.8, indicating rather heterogeneous scattering. Figure 7-4b was produced on CCRS's Polarimetric Workstation (PWS).
about 45°), with a high value of entropy H of about 0.8, indicating rather heterogeneous scattering. Figure 7-4b was produced on CCRS's Polarimetric Workstation (PWS).
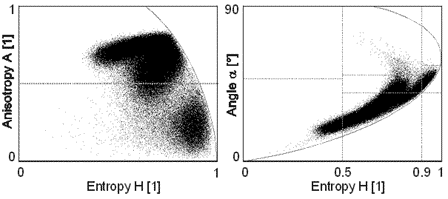
Figure 7-4a Scatter plots showing distribution of SIR-C ice data over the H / A /  classification space (Scheuchl)
classification space (Scheuchl)
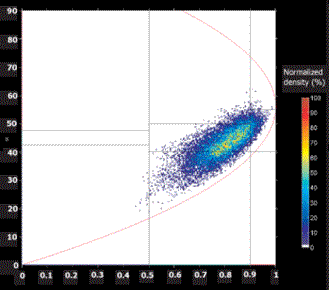
Figure 7-4b Scatter plots showing distribution of SIR-C ice data over the H / A /  classification space.
classification space.
Page details
- Date modified: