Motor Selection
a. Electrical Supply Considerations
The electrical supply distribution system must supply the correct voltage and have sufficient capacity to start and operate the motor load. Table 7 1 provides a cross comparison of nominal system voltage to show what one might find on a typical motor nameplate.
The limit to the supply voltage is dependent on the current required to operate the motor. For example, a 50 HP motor will require 150 Amps to operate at 208/120 volts, but requires only 50 Amps at 600/347 volts. Therefore, it would not be economically practical to provide motors beyond a certain HP rating for a given voltage when the conductor size becomes too large both in the supply to and within the motor.
Single Phase:
Single phase motors are rated for 120/240 volts at 60 Hz.
3-Phase:
3-phase motors up to 100 HP are available for 200, 240/460, 460 or 600 volts at 60 Hz. For 125 HP and up, they are available for 460, 600, 2400 or 4160 volts at 60 Hz.
Voltage and Frequency
Motors can be specified to operate on voltages and frequencies other than standard. An example of this is low voltage 400 Hz motors that are used in the aircraft industry, as well as some mine tool applications.
The nominal supply voltage of the power system and the utilization or nameplate voltage on the motor often differ. The following table (Table 7-1) shows the relation between motor nameplate voltage and the correct supply voltage for that motor.
| Nominal System Voltage | Motor Nameplate Voltage |
|---|---|
| 120 – 1 phase | 115 |
| 208/120 – 3 phase | 200 |
| 240 – 1 phase or 3 phase | 230 |
| 480/277 – 3 phase | 460 |
| 600/347 – 3 phase | 575 |
| 2400 – 3 phase | 2300 |
| 4160/2400 – 3 phase | 4000 |
The following should be considered when selecting a motor for a particular application:
- The mechanical requirements of the driven load.
- Motor classification.
- The electrical distribution system.
- Physical and environmental considerations.
The ultimate selection will be a motor available from a manufacturer that meets or exceeds the required specifications.
3-phase induction motors are designed to operate successfully with voltage variations of ± 10%. Table 7 2 shows the effects of a 10% variation on a typical Design B induction motor at full load.
| Characteristic | Voltage | |
|---|---|---|
| 110% | 90% | |
| Slip | -17% | +23% |
| Efficiency | +1% | -2% |
| Power Factor | -3% | +1% |
| Current | -7% | +11% |
| Temperature oC | -4% | +7% |
| Starting Torque | +21% | -19% |
| Starting Current | +10% | -10% |
The use of a motor with a non-standard or incorrect utilization voltage from the supply system should be avoided. For example, a motor with a nameplate voltage of 440 V is sometimes connected to a 480 V system. While the maximum allowable voltage for the motor is 484 V (110% x 440) there is no allowance for an upward supply voltage variation (for example, the utility can supply 500 volts and be within accepted tolerances) as the motor is already operating at its upward supply voltage limit. A motor of the proper voltage rating should be used, or a transformer should be installed to supply the correct voltage.
Phase voltage unbalance must be less than 1% for proper motor operation. A phase unbalance of 3.5% results in a temperature rise of 25% and a current increase of 6-10 times the voltage unbalance. These effects occur due to negative sequence currents flowing in the motor. Voltage unbalance is calculated as follows:
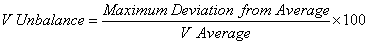
As an example, if line voltages were measured as 600, 585, and 609 volts, the average is 589 volts. The maximum deviation from average is 13 volts (598-585), and thus the voltage unbalance is (13/598) x 100 = 2.2%.
If a motor must be operated with a phase unbalance of greater than 1%, then the motor should be derated according to the following graph:
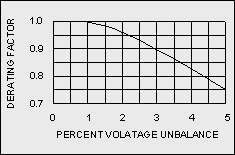
Figure 7-1: 3-phase Squirrel Cage Induction Motors Derating Factor Due to Unbalanced Voltage
A motor should not be operated if the phase unbalance is greater than 5%.
Frequency variation of up to 5% is permitted for normal motor operation. However, this should never be a problem if the system is supplied from a utility. Motor speed varies directly with the frequency of the power supply.
Power Factor
Most AC motors require reactive power from the supply system to develop magnetic fields. Measured in kVARs, reactive power does not provide any mechanical work.
Useful mechanical work is developed from real power supplied by the supply system and is measured in kilowatts (kW).
The supply distribution system provides both real and reactive power to operate the motor. The vector sum of real and reactive power is called the apparent power and is expressed in kVA.
The reactive component stays essentially constant whether a motor is lightly or heavily loaded. Therefore lightly loaded motors are said to have a lower power factor than a fully loaded motor. A facility with a very low uncorrected power factor is indicative of a significantly high number of under loaded motors.
If you are billed for kVA, then you are paying for the reactive power component and you are not getting any useful work. The measure of real power (kW) divided by total power (kVA) is defined as the "power factor." The highest power factor achievable is 1 or "unity" power factor and is often expressed as a percentage with 1 equal to 100%.
Industrial customers install capacitors to cancel the inductive component of motor loads to improve their power factor. In Figure 7-2, the vertical vector above the real power line represents the inductive component and the horizontal vector represents the real power. The hypotenuse vector equals the square root of the sum of the squared real and reactive vectors (See the equation following Figure 7-2). The vertical vector pointing below the horizontal line represents the capacitive reactance. When the capacitive reactance equals the inductive reactance, the two vertical vectors cancel each other out, leaving only the real power component (i.e. unity power factor). However, if capacitance exceeds inductance, a leading power factor will result which could result in over voltage and harmonic problems. To avoid this, capacitors should be switched on and off to match at the service entrance or better still installed at the motor load.
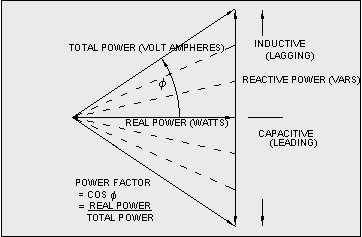
Figure 7-2: Power Factor Triangle
Text version figure 7-2
Power Factor Triangle
the vertical vector above the real power line represents the inductive component and the horizontal vector represents the real power. The hypotenuse vector equals the square root of the sum of the squared real and reactive vectors. The vertical vector pointing below the horizontal line represents the capacitive reactance. When the capacitive reactance equals the inductive reactance, the two vertical vectors cancel each other out, leaving only the real power component (i.e. unity power factor).
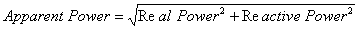
Voltage Flicker
Starting motors or other large loads causes a voltage drop on the supply system due to the effect of their high inrush currents on the circuit impedance. This may be perceived as a flicker in lighting circuits. As the motor comes up to speed, the current falls to normal operating levels and system voltage rises. This flicker becomes objectionable when the magnitude of the voltage drop and the frequency of occurrence exceed certain thresholds. This threshold of objection is shown on a voltage flicker curve (Figure 7-3).
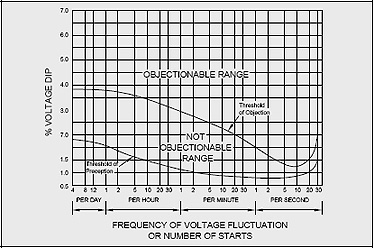
Figure 7-3: Voltage Flicker Curve
If the magnitude of voltage drop and the frequency of occurrence lie below the threshold of objection, but about the threshold of perception, people notice the light flicker, but generally do not find it irritating.
If the magnitude of the voltage drop and the frequency of occurrence lie below the threshold of perception, people do not generally notice any flicker.
Some electronic devices such as PCs, televisions and PLCs may not be able to tolerate voltage flicker as well as others. While some devices can ride through minor flicker incidents, others may lock up or suffer component failure.
As an example, consider a 5 HP motor supplied by a 208 V feeder which also supplies 120 V lighting circuits (Figure 7-4).
Assume: 5 HP motor
Full Load Amps = 16 A
Starting current = 96 A
Feeder impedance = 0.06 Ω
Calculate Feeder Voltage Drop:
Voltage drop along feeder = starting current (A) x feeder impedance Ω
=96A x 0.06Ω
= 6 V
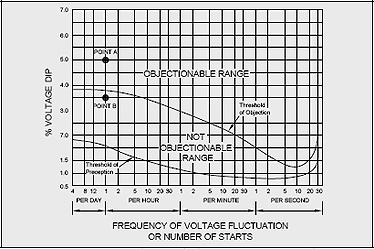
Figure 7-4: Voltage Flicker Curve - Example
The 6 V drop along the feeder is equal to 5% of the voltage on the 1320 V lighting circuit and causes a noticeable flicker.
If the motor is started once every hour then the point on the flicker curve is in the objectionable range (point A).
To correct this problem, the lighting circuits can be supplied from a separate feeder, or the voltage drop along the feeder can be reduced. In this case, a drop of 3.6% or less is not objectionable.
Supplying the lighting from a different feeder or upgrading the feeder is one approach that is often used.
A reduced voltage starter for the motor is another alternative and is often a very cost effective solution.
If the starting current is limited to 70% of its normal value by use of a reduced voltage starter, the voltage dip is 3.5% (70% x 5%) and the motor starting once per hour is not objectionable (Point B).
b. Motor Considerations
3-Phase Motor
Induction Motor Selection:
Wound rotor induction motors are often referred to as squirrel cage. They are considered the workhorse of the industry because of their relatively low cost, high availability, and minimal maintenance requirements.
3-phase squirrel cage induction motors in the 1 to 200 HP range are specified by their design type: A, B, C or D.
These standard designs are suited to particular classes of applications based on the load requirements typical of each class.
Wound rotor induction motors are useful in some applications because their rotor circuits can be altered to give the desired starting or running characteristics; however, they require brush servicing maintenance.
Table 7-3 can be used to help determine which design type should be selected.
Design B motors are by far the most common and satisfy virtually all applications, except where high starting torque or high peak loads are encountered.
Design A is rarely used in new applications as the starting current is higher than design B for virtually the same starting torque. Design A is included here for completeness only.
| Classification | Starting Torque (Percent Rated Load Torque) |
Breakdown Torque (Percent Rated Load Torque) |
Starting Current | Slip | Typical Applications |
|---|---|---|---|---|---|
| Design A and B Normal starting current | 100-200% | 200-250% | Normal | <5% | Fans, blowers, centrifugal pumps and compressor, etc., where starting torque requirements are relatively low. |
| Design C High starting torque and normal starting current. | 200 - 250% | 200-250% | Normal | <5% | Conveyors, crushers, string machines, agitators, reciprocating pumps and compressors, etc., where starting under load is required. |
| Design D High starting torque and slip. | 275% | 275% | Low | >5% | High peak loads with flywheels such as punch presses, shears, elevators, extractors, winches and hoists, oil-well pumping and wiredrawing machines. |
| Wound rotor | Any torque up to the breakdown value | 225-275% | Depends on starting torque. | Depends on Rotor resistance | Where high starting, or limited (2:1) speed are required and where high inertia loading must be accelerated. |
Synchronous Motor Selection
A synchronous motor is sometimes selected instead of an induction motor because of its operating characteristics. It is significantly more expensive and only used if it can be justified by the following considerations:
Speed:
Synchronous motors operate at synchronous speed with no speed drop over the load range. They should be selected if exact speed is required.
Power Factor Correction:
Synchronous motors can generate reactive power to correct poor supply system power factor while delivering mechanical power. When supplying reactive power they are said to be operating at a leading power factor.
Lower Operating Costs:
Synchronous motors are often more energy efficient than induction motors, especially in the larger horsepower ranges.
A general rule of thumb is that a synchronous motor should be selected where the horsepower requirement exceeds the speed (in RPM) of the motor.
Direct Current Motor Selection
DC motors are often selected where precise speed control is required, as DC speed control is simpler, less costly and spans a greater range than AC speed control systems.
Where very high starting torque and/or high over-torque capability is required, DC motors are often selected.
They are also appropriate where equipment is battery powered.
Single Phase Motor
Single phase motors are selected according to the type of load or application for which they are intended. Table 7 4 lists motor types, characteristics and typical uses for single phase motors.
| Type | Typical RPM | Starting Torque as Percent of Full-Load Torque |
Comparative Efficiency | Typical Applications |
|---|---|---|---|---|
| Shaded Pole | 1050, 1550, 3000 | Very Low 50-100% | Low | Small direct-drive fans and blowers. |
| Permanent Split Capacitor (PSC) | 825, 1075, 1625 | Low 75-150% | Moderate | Direct-drive fans and blowers |
| Split-Phase | 1140, 1725, 3450 | Low to Moderate 130-170% | Moderate | Belt-drive and direct-drive fans and blowers, small tools, centrifugal pumps, and appliances |
| Capacitor-Start | 1140, 1725, 3450 | Moderate to High 200-400% | Moderate to High |
Pumps, compressors, tools, conveyors, farm equipment, and industrial ventilators |
c. Driven Load Considerations
For a motor to drive a load properly, it must produce enough torque to accelerate from standstill to operating speed, and it must supply enough power for all possible demands without exceeding its design limits.
For example, a motor with inadequate starting torque for the connected load will either not turn or will act sluggishly during acceleration. The starting current may persist for too long and consequently trip overload protection. While running, an undersized motor may stall if the load suddenly increases (e.g. too many sheets fed into a paper shredder).
To specify the motor properly, certain characteristics of the load should be considered.
Motors must be sized to accommodate the running load's speed and torque requirements. Load types can be classified into different duty cycles describing operating time and load variations.
If replacing an existing motor is considered, monitoring the power input to the motor over a period of time will determine an optimum size. Inexpensive battery powered data loggers work well for load trending.
There are three general classifications of duty cycle that describe most motor loads: continuous, repetitive and intermittent duty.
Continuous Duty - Torque Constant
The majority of motor applications are continuous duty.
This cycle has essentially a constant motor load for an indefinitely long period of time.
Size motors for the horsepower requirement of the continuous load.
Repetitive Duty Cycle - Variable Torque
This motor application has various loads that are well defined and repeating. For example, a plastic injection molding machine.
For repetitive duty cycle loads, the motor rating is determined form the root-mean-square or RMS horsepower.
The RMS horsepower is calculated by the following equation:
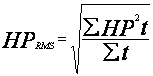
Text version RMS horsepower calculation
The RMS horsepower is the square root of the sums of the horsepower squared, times the time interval; divided by the sums of the time intervals.
The RMS horsepower is the square root of the sums of the horsepower squared, time the time interval; divided by the sums of the time intervals.
For example, consider the following horsepower-time curve (Figure 7-5).
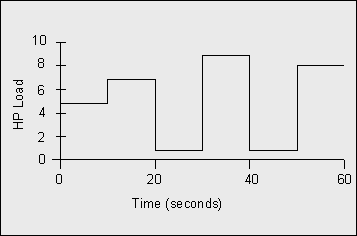
Figure 7-5: Repeating Duty Cycle Curve
For this load the time interval and load are:
| Time (sec) | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
|---|---|---|---|---|---|---|
| Load (HP) | 5 | 7 | 1 | 9 | 1 | 8 |
| HP²t | 250 | 490 | 10 | 810 | 10 | 640 |
The RMS horsepower is calculated as:
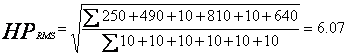
Text version - RMS horsepower calculation
RMS horsepower is equal to the square root of 250 plus 490 plus 10 plus 810 plus 10 plus 640 divided by 10 plus 10 plus 10 plus 10 plus 10 plus 10. This resolves to an answer of 6.07.
The next higher standard rating, a 7.5 HP motor would be the appropriate choice since 6.07 HP motors aren't available.
Intermittent Duty
This cycle alternates between indefinite intervals of load and no-load; load and rest; or load, no-load and rest. For example, a garage door opener.
Select motor so the horsepower rating of the motor matches the loaded power requirement.
d. Speed
e. Starting and Stopping
Frequency of starting and stopping. For frequent starts, ensure winding and core temperature do not exceed motor rating.
Starting torque requirement. Pay special attention to high inertia loads to ensure motor starting torque is adequate.
Acceleration restrictions. Ensure the motor driving the load reaches full speed quickly enough to avoid tripping the overload protection. Conversely, some loads require time to accelerate to full speed, e.g. a conveyor belt - a variable speed drive may be justified to achieve this and keep current lower when starting up.
f. Custom
Manufacturers' lines of "standard" motors offer models that suit most applications. Standard motors are less expensive, have proven engineering and are available on shorter lead times. However, motors can be ordered with myriad of variations to fit special applications where a standard motor is not suitable. Each motor supplier can provide specific information on availability lead time and price.
g. Environmental Factors
Usual Service Conditions
Motor ratings apply to motors operating under usual service conditions.
NEMA Standard MG 1 specifies usual environmental conditions as:
- Exposure to an ambient temperature in the range of 0°C to 40°C; when water cooling is used, in the range of 10°C to 40°C.
- Exposure to an altitude which does not exceed 3300 feet (1000 metres), (See MG 1-14.04).
- Installation on a rigid mounting surface.
- Installation in areas or supplementary enclosures which do not seriously interfere with the ventilation of the machine.
Unusual Service Conditions
The manufacturer should be consulted if the motor is to be operated in unusual service conditions.
NEMA standards specify typical unusual service conditions as:
- Exposure to:
- Combustible, explosive, abrasive, or conducting dusts.
- Lint or very dirty operating conditions where the accumulation of dirt may interfere with normal ventilation.
- Chemical fumes, flammable or explosive gasses.
- Nuclear radiation.
- Steam, salt-laden air, or oil vapour.
- Damp or very dry locations, radiant heat, vermin infestation, or atmospheres conducive to the growth of fungus.
- Abnormal shock, vibration, or mechanical loading from external sources.
- Abnormal axial or side thrust imposed on the motor shaft.
- Operation where:
- There is excessive departure from rated voltage or frequency, or both (See MG 1012.44 for alternating current motors and MG 1-16.64 for direct-current motors).
- The deviation factor of the alternating-current supply voltage exceeds 10%.
- The alternating-current supply voltage is unbalanced by more than 1% (see MG 1-12.45 and MG 1-14.35).
- The rectifier output supplying a direct-current motor is unbalanced so that the difference between the highest and lowest peak amplitudes of the current pulses over one cycle exceed 10% of the highest pulse amplitude at rated armature current.
- Low noise levels are required.
- Operation at speeds above the highest rated speed.
- Operation in a poorly ventilated room, in a pit, or in an inclined position.
- Operation subject to:
- Torsion impact loads.
- Repetitive abnormal overloads.
- Reversing or electric braking.
- Operation of a machine at standstill with any winding continuously energized, or of a short-time-rated machine with any winding continuously energized.
- Operation of a direct-current machine where the average armature current is less than 50 percent of the rated full-load Amperes over a 4-hour period, or continuous operation at armature current less than 50 percent of rated current for more than 4 hours.
h. Physical Factors
Enclosure
The enclosure for the motor should be chosen to protect it from the expected operating environment.
Table 7 6 lists standard enclosures as specified by NEMA.
| Types | Characteristics |
| Open: | |
| Drip-proof (ODP) | Operate with dripping liquids up to 15' from vertical |
| Splash-proof | Operate with splashing liquids up to 100' from vertical |
| Guarded | Guarded by limited size openings (less than ¾ in.) |
| Semiguarded | Only top half of motor guarded. |
| Drip-proof fully guarded | Drip proof motor with limited size openings. |
| Externally ventilated | Ventilated with separate motor driven blower, can have other types of protection. |
| Pipe ventilated | Openings accept inlet ducts or pipe for air cooling. |
| Weather protected type 1 | Ventilating passages minimize entrance of rain, snow, and airborne particles. Passages are less than ¾ in. in diameter. |
| Weather protected type 2 | Motors have in addition to type 1, passages to discharge high-velocity particles blown into the motor. |
| Totally enclosed: | |
| Nonventilated (TENV) | Not equipped for external cooling. |
| Fan-cooled (TEFC) | Cooled by external integral fan. |
| Explosion-proof (TEXP) | Withstands internal gas explosion. Prevents ignition of external gas. |
| Dust-ignition-proof | Excludes ignitable amounts of dust and amounts of dust that would degrade performance. |
| Waterproof | Excludes leakage except around shaft. |
| Pipe-ventilated | Openings accept inlet ducts or pipe for air cooling. |
| Water-cooled | Cooled by circulating water. |
| Water to air-cooled | Cooled by water-cooled air. |
| Air-to-air cooled | Cooled by air-cooled air. |
| Guarded TEFC | Fan cooled and guarded by limited size openings. |
| Encapsulated | Has resin-filled windings for severe operating conditions. |
Mounting and Base Considerations
Motors are generally mounted horizontally with feet attached to the floor, but other arrangements are common:
- Wall mounted
- Ceiling mounted
- Pedestal mounted
- Face mounted
- Flange mounted
The size and length of the shaft can be specified if the standard shaft types or materials are not suitable for the required mounting arrangement or machine configuration.
Insulation
The type of insulation used in a motor depends on the operating temperature that the motor will experience. Motors are specified by ambient temperature and insulation class.
Class A is an older obsolete classification. Class B is the current standard.
Class F and H are used for higher temperature applications and are often available as "standard" by many motor manufacturers.
Average insulation life decreases rapidly with increasing temperature. A cool running motor will have a much longer insulation life.
| Class | AC Motor DC. Motor W/1.00 S.F. Max. Total Temperature Range (Including Ambient and Temperature 110oCHot Spot) Range |
DC Motor Total Temperature Range |
|---|---|---|
| A | 105°C | 110°C |
| B | 130°C | 140°C |
| F | 155°C | 170°C |
| H | 180°C | 195°C |
Table 7-7 shows the maximum allowable stator winding temperature for an operating life of 20,000 hr and a maximum ambient temperature of 40°C.
As a general rule of thumb, insulation life doubles for each 10°C of unused insulation temperature capability. For example, if you design a motor to have a total temperature of 110°C (including ambient, rise, and hot spot allowance), but build it with a Class B (130°C) system, an unused capacity of 20°C exists. This extra margin raises the expected motor insulation life from 20,000 hrs to 80,000 hrs.
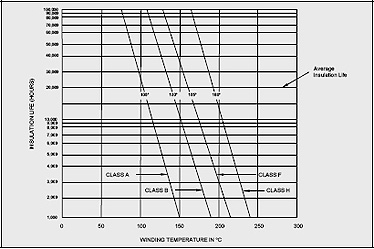
Figure 7-6: Insulation Life vs. Temperature
Service Factors
Motor service factor is an indication of the ability to exceed the mechanical power output rating on a sustained basis. A service factor of greater than 1.0 allows a margin for peak horsepower demand without selecting the next larger motor size. At an ambient temperature of 40°C, the standard service factor for integral HP motors up to 200 HP is 1.15.
Motor efficiency is usually reduced during operation at the service factor rating.
Service factors for higher temperatures or high altitude (>3300 feet) can often be specified where required.
Noise
If a motor is applied in an area where noise levels are of concern, motors equipped with plain bearings and specially designed ventilation systems are available. Plain bearings are quieter than roller or ball bearings.
If noise is a real issue, there are many active and passive technologies available to substantially reduce audible noise. Motors inherently have repetitive noise emissions and therefore lend themselves to noise cancelling techniques. Producing an equal and opposite phase waveform of the noise effectively cancels or substantially reduces motor noise. Noise cancelling headphones for air passengers use these techniques to effectively block out engine noise.
i. Efficiency and Economics
When selecting a motor for a particular application, both its capital cost and the cost of energy for operation should be considered.
Energy Costs
The cost of electricity to run a motor for one year can easily exceed the purchase price of the motor.
Figure 7-7 shows the operating cost for a typical standard efficiency 20 HP motor operating for one year at 88% efficiency.
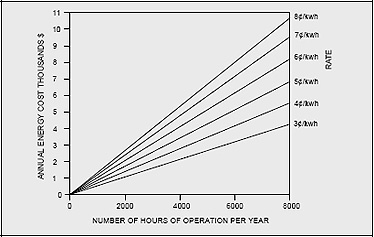
Figure 7-7: Annual Operating Costs of a 20 HP Motor
Since the operating cost over the life of a motor is often many times its purchase price, small differences in motor efficiency can yield significant savings.
Motor Efficiency
The efficiency of a motor is the ratio of mechanical power output to the electrical power input and is usually expressed as a percentage.
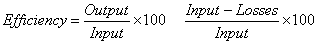
Electric motors are generally efficient devices, but with enhanced materials and improved design they can operate with fewer losses. These are referred to as energy efficient motors because they produce the same mechanical output power using less electrical input power than a standard motor.
Motors can experience losses, whereby they consume electrical energy, but do not contribute useful mechanical energy output.
They occur in five areas:
- Core losses
- Stator losses
- Rotor losses
- Friction and windage
- Stray load losses
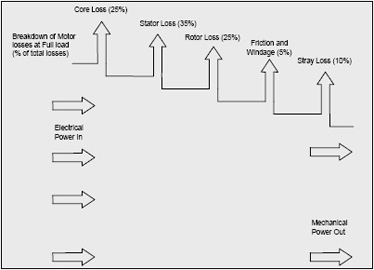
Figure 7-8: Motor Losses
Core losses are comprised of Hysterisis losses (the energy required to magnetize the core) and eddy current losses in the stator core (magnetically induced circulating currents). Core losses make up about 25% of the total losses.
Stator losses are due to the I2R heating effect of current flowing through the resistance of the stator windings. They account of approximately 35% of the total.
Rotor losses are caused by the I2R heating effect in the rotor. Rotor losses are responsible for about 25% of the total.
Friction and windage losses include bearing friction, wind friction on the rotor assembly, and the motor's cooling fan load. They make up about 5% of the total.
Efficiency and Motor Sizing
The efficiency of induction motors varies with load.
Peak efficiency occurs between about 60% and 100% of full load depending on design, and drops significantly below about 30% of full load (Figure 7-9).
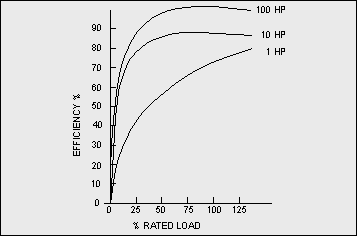
Figure 7-9: Typical Motor Efficiency vs. Load
Good engineering practice dictates slightly over-sizing a motor for the following reasons:
- To allow for an increase in production
- To accommodate load fluctuations and overloads
- To accommodate the increase in load as the driven load wears
- To increase motor operating life because of lower winding temperatures.
Sizing a motor for operation at about 75% of full load provides what is generally considered to be a reasonable margin. A service factor of 1.15 allows an additional 15% margin over full load to accommodate short term peak load conditions.
Induction motors should not be grossly oversized (<50% load) as the initial cost and energy costs are greater and the power factor and efficiency are lower.
Life Cycle Cost
An electric motor can consume up to ten times its purchase cost annually over its lifetime which can range from 15 to 25 years or more. Improvements in efficiency can result in substantial savings in life cycle cost which includes the capital and operating costs.
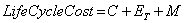
Where:
C = initial capital cost plus installation
ET = total energy cost = Hr/yr x $/kWh x avg. kW x years
M = total maintenance cost = annual $ x years
More complex calculations include discount factors, inflation, energy price increases etc., all brought back to a present value. However, since energy is the most significant factor in lifecycle cost, simple comparisons can be quickly made using this formula.
For example, a 10 HP motor operates 50% of the time at an average output of 7.5 HP. Its efficiency is 88%. Purchase price is $700 and installation is $100. The motor is expected to last 10 years and cost $30/year to maintain. Electricity price is $0.05/kWh
Energy consumption would be as follows:
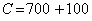
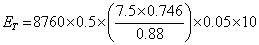
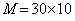
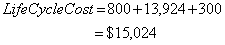
Performing the same calculation for an energy efficient motor (93%) that costs $150 more to buy would yield a lifecycle cost of $14,325, a saving of $699.
Motor Loss Reduction
Stator and rotor I²R heating losses are minimized by reducing the resistance of their respective windings. This is achieved by increasing cross sectional area, using higher conductivity materials or both.
Core losses are reduced by employing a high grade steel in the core laminations. This is generally achieved by increasing silicon content of the steel.
Thinner core laminations result in lower eddy core losses.
Increasing the cross sectional area of the stator and rotor lead to lower magnetic flux levels and thus lower Hysterisis losses.
Frictional losses are reduced with the use of smaller or better bearings.
Windage losses are minimized by using smaller fans. Even so, energy efficient motors usually run cooler than standard motors.
Energy Efficient vs. Standard Motors
Typical energy efficient motors are generally 1.5% to 8% more efficient than their standard motor counterparts with efficiency gains as high as 12% in the 1 HP range (Figure 7-10).
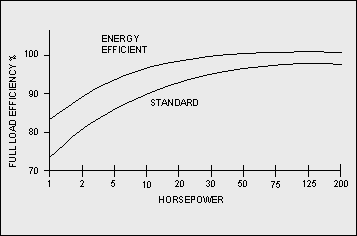
Figure 7-10: Typical Efficiencies of Standard and Energy Efficient Motors
There is quite a variation among different manufacturers as to how the qualitative terms "High Efficiency," "Premium Efficiency," or "Energy Efficient" 3-phase induction motors are applied. CSA Standard C390 (1993) states that an energy-efficient 3-phase induction motor is a motor rated from 1 to 200 HP, for which the nominal efficiency rating, at 75% or 100% of the rated load, is equal to or greater than the efficiency values shown in Table 7 8. CSA C390 (1993) is the recognized standard in Canada.
Other efficiency rating standards are described in the following paragraphs, including NEMA's voluntary premium efficiency program.
| Horsepower | 5 | 7.5 | 10 | 15 | 20 | 25 | 30 | 40 | 50 | 75 | 100 | 125 | 150 | 200 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ODP 1200 RPM | 87.5 | 88.5 | 90.2 | 90.2 | 91.7 | 92.4 | 93.0 | 93.0 | 93.0 | 93.6 | 94.1 | 94.1 | 94.5 | 94.5 |
| TEFC 1800 RPM | 87.5 | 89.5 | 89.5 | 91.0 | 91.0 | 92.4 | 92.4 | 93.0 | 93.0 | 94.1 | 94.5 | 94.5 | 95.0 | 95.0 |
Efficiency Ratings
Standardized tests are used to establish motor efficiency and performance.
Manufacturers use a dynamometer which loads the motor and measures the input and output power to test for efficiency.
There are three distinct standards commonly used to measure motor efficiency:
- CSA C390 (IEEE 112 method B)
- IEC 34-2 (British BS-269)
- JEC-37
There are some differences among these three methodologies, but the main difference is in the determination of stray load losses (Ref. 19).
IEEE 122 Method B determines the stray load losses through an indirect process. The IEC standard assumes stray load losses to be fixed at 0.5% of input while JEC standard assumes there are no stray load losses. Therefore, motor efficiencies determined by different standards are not comparable. Differences can be 5 percentage points or more.
Generally, CSA C390 (IEEE 112 Method B) is considered to be the most accurate method. Future harmonization among standards is likely, but will take time to implement.
NEMA has implemented a voluntary program which permits manufacturers to label their motors as "Premium Efficiency" if they meet or exceed minimum levels set by NEMA (NEMA Premium™, MG-1 2003 voluntary standard applicable to motors of 1 to 500 HP). Table 7 9 illustrates the advantage of premium efficiency over an energy efficient motor in terms of energy savings for a selection of motors.
| Full Load Efficiency % | Annual Savings from Use of a NEMA Premium Motor | ||||
|---|---|---|---|---|---|
| Horsepower | Energy Efficient Motor | Premium Efficiency Motor | Relative Energy Saving | Annual Energy Savings kWh | Dollar Saving $/year |
| 10 | 89.5 | 91.7 | 2.2 | 1200 | 60 |
| 25 | 92.4 | 93.6 | 1.2 | 1553 | 78 |
| 50 | 93.0 | 94.5 | 1.5 | 3820 | 191 |
| 100 | 94.5 | 95.4 | 0.9 | 4470 | 223 |
| 200 | 95.0 | 96.2 | 1.2 | 11,755 | 588 |
* Based on purchase of an 1800 RPM TEFC Motor with 8000 hr/year operation at 75% load at $0.05/kWh – source Motor Systems Tip Sheet #1 • September 2005 – US DOE Publication (Ref. 22).
In Canada, induction motors between 1 and 200 HP sold after 1998 must meet the minimum efficiency standards set in the CSA Standard CAN/CSA-C390-98. Such motors are called EPAct motors.
In recognition that motors are often part of an OEM piece of equipment, minimum efficiency requirements are being set (e.g. EER for air conditioners). This assures that the manufacturer will optimize overall efficiency in their design.
When comparing motor efficiencies, the comparison should be based on the "Nominal Efficiency" of the motor using one of the above test methods.
Free software is available on-line to help in selecting energy efficient motors.
In Canada, "CanMOST" (Ref. 8) is a good program to use. CanMost was derived from "IMSSA" (International Motor Selection and Savings Analysis) software, an international version of the successful MotorMaster+, developed by the U.S. motor energy-management software Washington State University Extension Energy Program (See Recommended Weblinks). The software is easy to use, comprehensive and up to date with present motors.
CanMOST's database is comprised of:
- Data on 25,000 North American motors
- The European Database of Efficient Electric Motor Systems (EuroDEEM), with 18,000 European motors
- Data on some 575 volt motors that are available only in Canada
Selecting Energy Efficient Motors
Because energy efficient and premium efficiency motors use more and better materials, they are also more expensive.
Premium efficiency motors should be selected when the cost premium over an energy efficient motor is recovered through reduced operating costs over a reasonable period of time.
Applications with high annual running hours and average to high loading are good candidates for energy efficient motors.
The operating cost of an electric motor can be calculated by knowing the horsepower rating of the motor, the motor loading, annual hours of operation and the blended electricity rate. The "blended" rate is an average electrical rate which takes into account both the demand and energy charge. The simplest method of obtaining a blended rate is to divide the total electric bill by the kWh consumed during the billing period. The resultant $/kWh provides a ballpark number for comparative purposes.
Utility billings can vary significantly and the number of line items can include kW demand, power factor, time of use, debt retirement charges, etc. An infrequently used motor operated coincidentally with the customer's peak could have a significant impact on the operating cost in terms of $/hour of operation due to the resultant peak demand charges which would overshadow the $/kWh charge.
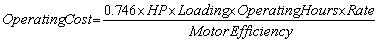
If the actual motor loading is not known, an estimate of 65% can be used.
The bottom line is that you should contact your local utility to help you determine the actual cost of operating your motor.
Motors with different efficiencies can be compared on an economic basis by calculating the annual operating costs and comparing these savings to the price differential between the motors.
The most common economic analysis used for electric motors is a simple payback analysis.
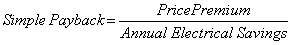
For example, if a premium efficiency motor cost $400 more than a standard motor and is expected to save $300 per year in electricity, the simple payback would be 400/300 = 1.33 years.
Companies generally accept a payback in the range of 1 to 2 years or less. Longer paybacks may still be acceptable for other users including homeowners.
Another way to estimate savings is as follows:
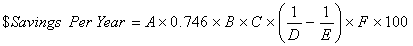
Where:
- A=Motor Nameplate Horsepower
- B=Total Dollar Cost Per Kilowatt
- C=Hours Run Per Year
- D="Standard" Motor Efficiency-%
- E="Premium" Motor Efficiency-%
- F=Load Factor (avg. load HP/nameplate HP)
Therefore, if a 40 HP, 94.5% premium efficiency motor operating at 75% of rating, 6000 hours per year, the annual savings compared to a standard 89% efficient motor will be:
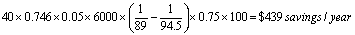
Annual savings will increase in proportion with electricity price, running hours per year, and load factor.
Assessing Existing Motor Inventory
Taking an inventory of existing motors can form the basis for an efficiency improvement plan. Sizes, type, duty cycle, and loading are all important factors to record. The motor's history including previous rewinds (if known) should be recorded. Monitoring motors with high running hours helps establish optimum sizing.
The largest motors with high duty cycles should be scrutinized for energy efficient replacements. Substantially oversized motors would also be likely candidates if the run time justifies the change. Previously repaired motors with high run times should be tested for efficiency using a dynamometer or equivalent means. Such testing would be limited to very large motors for economic reasons. Armed with this information, sound business cases can be developed to compete for capital improvement funding.
Having a motor inventory helps in deciding whether to buy new or to repair a failed motor. Older small motors are typically not worth repairing given the higher efficiency products available today.
Power Factor Issues
Motor power factor also drops significantly below 75% load (Figure 7-11). A lightly loaded motor will typically have a poorer power factor, resulting in a higher kVAR input than a motor more closely matched to the load.
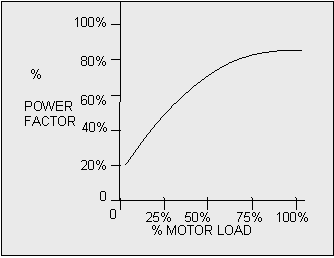
Figure 7-11: Typical Power Factor vs. Load²
Therefore, if you are being billed in kVA, your cost of running the motor will be more than the work (kW) it is doing at 50%. See section 6A ii above for a more detailed explanation.
Previous: Advanced Motors | Table of Contents | Next: Motor Controls
Page details
- Date modified: